ローラーコースターの最高速度を考える

Author: Yu Shioji (塩地 優)
Article type: Article(研究)
Article number: 240011

2024年10月に、リヤド近郊に世界最速、250 km/hのローラーコースターがオープン予定です。高さや全長など、様々な項目で圧倒的な世界一となるコースターですが、実は速度はこれまでの記録と10 km/hしか違いません。もちろん、この領域の10 km/hというのは大きな差ではあるのですが、いよいよ速度の限界が近づいているようにも見えます。果たして、速度の理論的限界はどこにあるのか。ここでは、世界最速予定のコースター、Falcon’s Flightを例に、人体の負荷等は無視して、機械的な部分でローラーコースターの最高速度を考えてみたいと思います。

純粋に機械的なネックはベアリング
ベアリングの許容回転数
車輪の外径
車輪の発熱
ジオメトリ由来の制約
加速機構の制約
まとめ
参考文献
引用方法
利益相反

純粋に機械的なネックはベアリング

速度を上げれば上げるほど、当然車体にかかる負荷は高くなります。ただ、その負荷というのは、加速をゆっくりにしてあげることで緩和することができます。あまりローラーコースターとして楽しくはありませんが、ゆっくりゆっくりと加速していけば、車体の負荷的には限界は無い(当然、音速の壁はありますが)に等しくなります。

鉄道の場合は、おおよそ360 km/h程度が常用の最高速度と言われますが、実験での一時的な速度では、500 km/hといった値も出ます。その制約は、鉄の車輪と鉄のレールを用いていることによる、摩擦の小ささに由来します。ですから、ナイロンやポリウレタンなど、より摩擦の大きな車輪を用いるローラーコースターの場合には、車輪の材料に由来する限界速度は、より高いと考えられます。

豊富な資金力があれば圧倒的な高速を実現することはできるのですが、現実には主としてコストの観点から最高速度に制約が入ります。

では、そうした観点で最高速度を決めるのはどこかというと、車輪のベアリングと車輪サイズです。ベアリングには、許容回転数というものがあります。また、ベアリングが許容回転数で回転したときに、どの程度の速度になるか、というのは車輪の外径で決まります。ですから、この2つのパラメータがローラーコースターの最高速度を決めるのです。

ベアリングの許容回転数は、各輪軸ごとの負荷によって、車輪の外径は、転がり抵抗による制約から決まります。ここでは、それぞれの制約を、主輪と側輪の２か所について考えてみることにします。

側輪を考えるのは、一般に最高速度付近で左右両方の側輪がレールから離れた状態にあるとは考えにくいためです。底輪については、最高速度の状態では、一般に正方向の加重(下向きの加重)がかかっているため、常時底輪を押し付けるタイプで無ければ、離れている可能性が高いと考えられます。一方で、側輪は左右両方の車輪がレールから離れることは、まずありません。したがって、最高速度を制約する要因になり得ると考えられます。

ベアリングの許容回転数

ベアリングの許容回転数は、ベアリングの大きさによって決まります。ベアリングが大きい方が許容回転数は小さく、ベアリングが小さい方が許容回転数は大きくなります。

このため、最高速度を上げるためにはベアリングを小さくした方が良いということになります。では、どういった場合にベアリングを大きくしなければならないかというと、荷重が大きい場合です。大きな荷重に耐えるためには、ベアリングを大きくしなければなりません。ですから、基本的には許容加重と許容回転数がトレードオフの関係にあるとお考え下さい。

それでは、必要加重を主輪と側輪のそれぞれについて考えてみましょう。日本の法規の場合、車輪の安全率は4以上と定められています[1]。最大垂直加重を3G、水平横方向の荷重を1.5Gとしましょう。この垂直加重は、垂直ループが無ければ十分な値、横方向の荷重はよほど横に振り回すようなコースターでなければ十分な値です。そうすると、主輪は静荷重の12倍、側輪は静荷重の6倍が、ベアリングに求められる許容加重になります。

主輪は左右2輪ずつ、合計4輪で1両の荷重を支えます。側輪は、カーブでは片側2輪で1両の荷重を支えることになります。ですから、それぞれ1輪あたりに必要な許容加重は同じで、荷重の3倍になります。

また、荷重割り増し係数が通常のローラーコースター(鉄車輪≒木製ではないもの)は1.5と定められています。乗客の標準体重は65 kgを採用します。65 ㎏×4人＋車体重量300 kgを想定して、素の荷重が560 kg。割り増し係数を考慮して、840 kg。車輪1輪あたり、その3倍がかかりますので、2,520 kgとなります。

ベアリングには許容回転数の大きいものを選ぶことにしますと、例えばNTN社製のアンギュラ玉軸受けで、定格荷重25 kN以上のものの中では、例えば内径60 mm, 外径95 mmのものをグリスで使用すると、許容回転数が7,200 rpmとなります[2]。

車輪の外径

車輪の回転数が同じであっても、車輪の外径が大きくなるほど最高速度は上がります。

前述のFalcon’s Flightは、おそらく側輪の直径が20 cm程度だと思われます。したがって、外周が20 × 3.14で、62.8 cm。1分間に7,200回転というベアリングの許容回転数をかけると、62.8 cm × 7200 rpm = 4,520 m/min。これを時速に直すと、271 km/hとなります。最高速度が250 km/hですので、ギリギリの設計ですね。

ちなみに、一般的なローラーコースターはベアリングにグリス潤滑を用いますが、世の中にはオイル潤滑を用いているものもあります。そうすると、許容回転数は2割程度上昇しますので、最高速度も324 km/h程度にまで上昇します。

オイル潤滑したベアリングを用いている車輪の例

一方、主輪は40 cm以上の大型のものを使用しています。外径40 cmの場合で、許容最高速度は542 km/hとなりますので、主輪は回転数自体が速度を制約することはありません。

では、いったい何が車輪の外径を決めているのでしょうか。

外径の上限を決めているのは、現実的には、メンテナンスコストだと思われます。公開されているローラーコースター向け車輪の価格は少ないのですが、例えばTechnicaのサイトを参照しますと、外径20 cmの車輪はベアリング付きで140ポンド[3](2024年2月現在、約2万7千円)、外径40 cmの車輪はベアリング無しで816ポンド[4](同、約14万7千円)です。やや高いようにも感じますが、公開されている数値が他にないため、この値段を採用することにします。

例えば、1両あたり4人乗り、5両編成のローラーコースターを考えます。1両あたり、左右2輪ずつ、合計4輪ずつの主輪、側輪、底輪があります。1編成あたり、主輪、側輪、底輪はそれぞれ4輪×(5+1)両で、24輪ずつということになります。両数が5+1となっているのは、ローラーコースターは一般にトラクターのように後輪だけしかない状態になっていて、先頭に座席のない車輪が1両分必要になるためです。

主輪が40 cm, 側輪と底輪が20 cmであれば、147,000円×24輪 + 27,000円×48輪で、1編成の車輪交換にかかるコストは、4,824,000円です。一方、主輪と側輪が40 cm, 底輪が20 cmの場合、147,000円×48輪 + 27,000円×24輪で、1編成の車輪交換にかかる費用は7,704,000円です。その差は288万円。2編成所有していて、年に1度車輪交換をする場合、メンテナンスコストに576万円の差を生じます。

ですから、許容される範囲で最も小さい外径の車輪を使いたい、というニーズを生じます。

車輪の発熱

外径の下限は、前述の最高速度に加えて、車輪の発熱も制約となります。車輪のレールとの接触面に用いられるポリウレタンは、常用可能な温度が、どんなに高いものでも100℃程度です。

一例として、実測ではなく有限要素法によるシミュレーションの結果ですが、[5]を参照しますと、最高速度約50 km/h, 全長341 mのコースターで、外径250 mmの車輪を用いると、車輪温度は20℃から60℃まで上がると報告されています。外径を380 mmにすると、最高温度は42℃まで低下します。

発生する熱量は、おおよそ速度の2乗に比例します。速度が50 km/hから250 km/hまで上昇すると、熱量は25倍発生することになります。当然、車輪1輪あたりにかかる負荷にも依存するので、単純な比較は難しいのですが、速度も全長も10倍以上となると、車輪に求められる要件も大幅に厳しくなります。一方で、速度が上がると風による冷却効果も高まりますし、外気温、レール温度等にも左右されますので、それを考慮に入れる必要があるのですが、大雑把には、外径約40 cmだと間違いなく100℃を超えます。実際には、Falcon’s Flightは空冷効果を考慮した車輪形状や、ウレタンの厚み等を工夫することで、温度上昇を緩和していると思われます。

車輪をファンにより冷却している例

一方で、側輪には負荷がほとんどかかりません。最近のローラーコースターでは、横Gが発生する場面はほとんどないため、許容荷重の面で大きな値を採用する必要はあっても、温度上昇の問題を懸念する必要がありません。ですから、側輪には許容回転数の観点から許容される最小の車輪を用いることができるのです。

以上より、主輪の制約としては、ベアリングの許容回転数よりも、発熱の問題の方が大きいことがわかります。ただし、これもあくまでコストの問題です。車輪を大きくしていくことで、発熱の問題は大幅に緩和されます。車体下に大きなスペースを必要とするようになりますが、一般的なアッカーマンタイプであれば、車輪可動範囲は広くないので、座席下などのスペースを活用すれば対応可能です。

ジオメトリ由来の制約

念のため、ジオメトリ面で側輪の外径を規制する要因が無いことを確認しておきましょう。

車輪の外径が大きくなると、車輪間距離が広くなって、特に側車輪に要求される可動域が大きくなります。車輪になぜ可動域が必要なのか、については下記をご参照ください。

ローラーコースターがカーブを曲がる方法

ローラーコースターがカーブでどのように曲がるのか、イメージできますか? 実は、カーブでの車輪の動きはそう簡単ではありません。どのように複雑で、どのような工夫がされているのか、詳しく解説しています。

実は、必要可動域は、上記で述べられているものよりも広くなります。上記、アッカーマン型のジオメトリを有するローラーコースターでは、アッカーマン由来の必要可動域は、最小曲率半径が5 m, 2本のレール間距離(外寸)が1 m, 車両長さが2 mの場合で(左右あわせて)20.8 mmとなります。これに加えて、車輪が回転軸からズレて設置されていることに由来する可動域を必要とします。これは車輪の外径に依存しますので、車輪の外径と、必要可動域との関係を図1に示します。

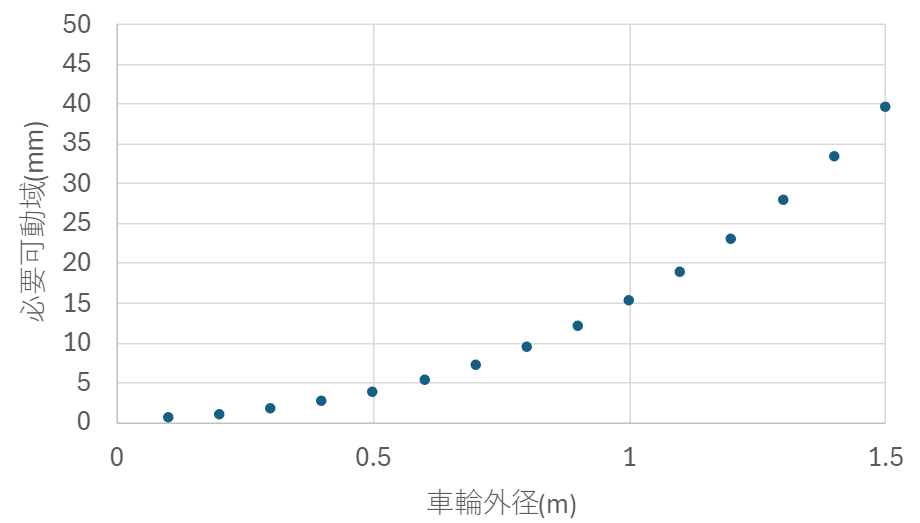
図1 車輪外径と必要可動域の関係

これを見ると、車輪外径が20 cmの場合で追加可動域は約1 mmしか必要としていません。車輪外径が40 cmの場合でも約2.6 mmですので、車輪外径を規定しているのは、車輪の回転軸からのズレに由来するものではないであろう、ということがわかります。ただし、アッカーマン型ではなく、ボギー台車タイプのジオメトリを有する場合には注意が必要です(ボギーとアッカーマンについては、上記「ローラーコースターがカーブを曲がる方法」を参照ください)。ボギータイプでは、側車輪に可動域を設けないことが一般的です。ですから、側車輪の外径が20 cmの場合で約1 mm, 40 cmの場合で約2.6 mmの遊びが必要になります。遊びが大きくなると、乗り心地の悪化や衝撃による車体の劣化につながりますので、これが理由で側車輪を大きくしたくない、あるいは最小曲率半径を大きくしたいという要求が発生します。

加速機構の制約

以上述べたもののほかにも、速度を制約すると考えられるものはあります。

1つは、リニア加速(LSM)のパワーです。Falcon’s Flightでは、既に水冷LSMユニットを700基用いています。出力を上げるには、まずは冷却能力の強化が必要ですし、また、鉄道よりも走行抵抗の大きいローラーコースターを加速させるには、より大きな出力を必要とします。これに対して、ローラーコースターは磁石の搭載スペースに限りがあるため、強力なLSMを使いにくいという懸念があります。Falcon’s Flightは、既に下り坂とLSM加速を組み合わせるという荒業で、何とかトップスピードを記録しています。

LSMの推力は、車体の重量見積もりが正確ではない場合、加速度から導き出す方が真値に近いはずです。様々なLSMコースターを見ていくと、おおよその加速度として、0-50 km/hの加速が1秒、0‐80 km/hの加速が2秒、0-95km/hの加速が3秒といったところが一般的な値だと思われます。ちなみに、富士急ハイランドの高飛車は、100 km/hまで2秒で加速しますが、通常のローラーコースターはLSMが1列であるのに対して、高飛車は2列あるツインタイプです。乗車定員が多いためにツインになっていると思われますが、その結果として単位重量当たりの推力も上がっています。

一方で、走行抵抗はおおよそ速度の2乗に比例する、としておきましょう。そうすると、加速中の運動方程式は、ma = f(LSMの推力) – kv^2となります。こういった運動方程式の解法は、例えば[6]をご参照ください。初速を0とした時の解を求め、変数を上記条件から決めると、図2のグラフのようになります。

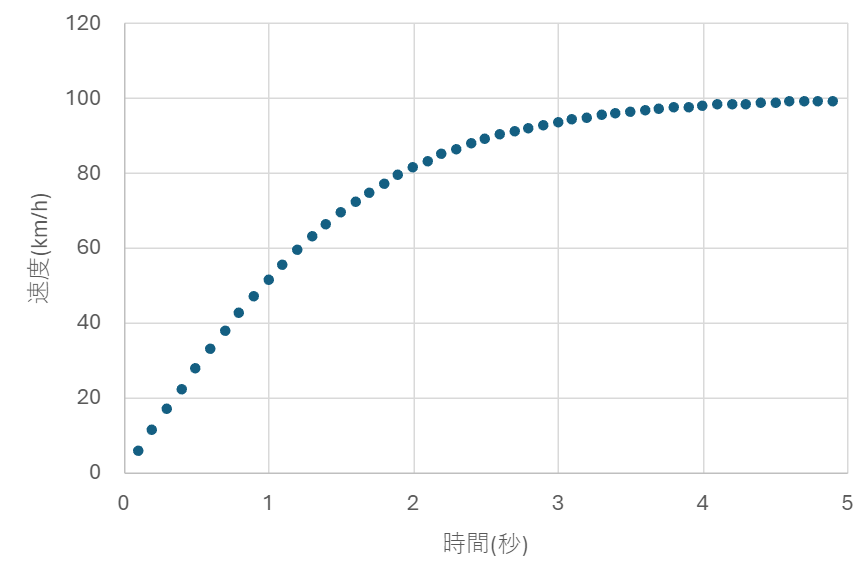
図2 LSM加速時の時間と速度の関係

これを見る限り、高速側の伸びが悪く、100 km/h超程度で頭打ちになることがわかります。これはモーターに共通する特性の問題で、低速側のトルクは良いのですが、高速域のパワーが無いため、速度が伸びない、高速で電費が悪いといった問題を生じます。ですから、LSMで加速をしようと思うと、どうしても速度に上限があります。

重力による落下で加速する場合も同じような問題をはらんでいて、高さを増していっても、走行抵抗とのバランスによって、どこかで速度が頭打ちになってしまいます。

ただし、これはあくまでも設計上の懸念であって、技術的にクリアできない課題ではないと考えます。走行抵抗は、車両の空力や車輪の転がり抵抗によって大きく変わります。また、LSMの問題も、例えば上述の通りツインにしたり、あるいは冷却効率を上げて出力を上げたり、奥の手として、車体側に(場合によっては超伝導の)電磁石(と冷凍機)を搭載することで、コストはかかりますがクリアが可能です。これから先、新たに作られるとは考えにくいですが、既に油圧方式では平坦路で最高速度240 km/hを記録していますので、これと下り坂を組み合わせるなどの方法でも、最高速度の更新は十分に可能だと考えられます。

まとめ

以上より、速度の上限は、側輪の回転数上限と、主輪の温度上昇によって決まることがわかりました。いずれもコストの問題が主因となっていて、速度上限が決まってしまいます。

主輪は外径40 cm程度までであれば、量産された製品が存在しますが、それを上回り、かつ冷却にも気を使う必要がある場合、特注品になると思われます。その場合、車輪価格が1輪あたり数十万円といった極めて高価なものになると考えられます。年間の車輪メンテナンス費用だけで1,000万円オーダーになってくると、導入できるパークは限られてしまいます。ですから、現状の250 km/hというのは、経済的にはほぼ上限であると考えられます。

なお、14人乗りのコースターで、所要時間を3分と仮定しますと、1,000人/時の効率を実現するには4編成が必要になります。そうすると、主輪だけでメンテ費用が2,000万円/年以上になると思われます。これを顧客負担にしますと、毎日10時間フル稼働して、年間365日稼働で1人あたり約5円。例えば、平均稼働率が半分程度で、1日8時間、年間200日の稼働にまで落ちると、1人あたり約25円。初期投資に比べれば微々たるものですが、フリーパスで繰り返し乗る人が出てくると、経営には重くのしかかってきます。

ですから、最高速度250 km/hであっても、中東以外の国にできることは無い、北米を含む一般的な遊園地において許容される上限速度は150 km/h程度である、というのが筆者の見解です。なお、例えばド・ドドンパは180 km/hを超える速度ですが、ポリウレタン車輪ではなく、ゴムタイヤを履いていますので、その観点からは一般的なローラーコースターの部類には入りません。非常に転がり抵抗が大きく、速度減衰が早いため、アップダウンなどのコースターらしいコースレイアウトを作りにくい、という課題があります。