Author: Yu Shioji (塩地 優)
※当サイト内の論文・解説等は、すべて著者個人がデータ収集、解析、考察を行ったもので、いかなる文言も当会を代表するものではありません。
Article type: Article (研究)
Article number: 250014
遊園地やテーマパークのアトラクションには、様々な制約があります。特に、キャパシティという視点で見ると、遊園地はアトラクションの数にも、キャパシティの分散にも強い制約がかかっていることがわかります。遊園地やテーマパークを構想する際にも、リニューアルを考える際にも、極めて重要な観点ですが、この点を見過ごしたが故に、運営がうまくいかなかった遊園地も少なくありません。ここでは、一般的な遊園地において、どのような制約があるのかを見ていくことにします。
数式ベースで議論を進めますが、中学校レベルの多項式の知識があれば理解でき、高校レベルの多項式の知識があればグラフの形までイメージできるレベルで進めていきます。
前提条件
まず、以下の試算における前提条件をあげておきます。
対象とする遊園地は、半日~1日の滞在を想定する、郊外型の遊園地です。都市型の遊園地の場合には、アトラクション数が少なく、いずれも大キャパシティで、想定滞在時間が1~数時間というパターンも考えられますが、ここではそうした遊園地は考えないことにします。
簡単のため、アトラクションは、3種類のキャパシティに分類されることとします。また、それぞれキャパシティの比率は一定になるようにします。キャパシティが最小のものをaとしたとき、中間のものはax, 最大のものはax2で表します(x>=1)。これは、500人/h, 1,000人/h, 2,000人/hのアトラクションを揃える大手テーマパークをイメージしていますが、数値や比率はこれに限りません。なお、ここでいうキャパシティとは、理論効率ではなく、実効効率のことです。1時間に、実際に何人が乗れるかを示す数値です。
アトラクションの数は、キャパシティごとに異なることにしますが、アトラクション数の比率は一定になるようにします。キャパシティが最小のaであるアトラクションの数をby2としたとき、キャパシティがaxのアトラクションの数はby, キャパシティがax2のアトラクションの数はbと表します(y>0)。この比率一定という前提は、大手テーマパークの場合は特に自明ではありませんが、遊園地の場合はローラーコースターなどの大規模な遊具と、中規模の遊具、小規模の遊具と小さくなるにつれて増加傾向になることが多いため、このような仮定を置いています。
定式化と範囲設定
では、これらの前提条件をもとに、数式を立てていきましょう。
全アトラクションの、1時間当たりのキャパシティの和は、
ab(x2+xy+y2) ……(1)
となります。営業時間を8時間とすれば、1日にアトラクションを体験できる延べ人数は、
8ab(x2+xy+y2) ……(2)
となります。パークのキャパシティを、アトラクション乗車回数の期待値から決めていきましょう。アトラクション乗車回数の期待値は、1日にアトラクションを体験できる延べ人数を、パークのキャパシティで割れば、おおよそ求まります。
アトラクションは、どの程度の数体験できれば満足でしょうか。半日かけて、体験時間数分~15分程度のものが3個では、少なすぎると感じるでしょう。5個であれば、少ないけどまぁ、くらいの感触ではないでしょうか。チケット料金から考えますと、例えばフリーパスが6,000円、入園料1,200円として、差額4,800円分が乗り物代としましょう。各アトラクションの利用料が500円~1,000円で、平均単価が700円であれば、アトラクション7個乗車で元が取れることになります。ここでは、式の単純さから、営業時間8時間で、アトラクション8個乗車を狙いの期待値としましょう。すると、パークのキャパシティは、
ab(x2+xy+y2) ……(3)
となります。
どんな混雑日でも、1日に8個のアトラクションに乗車できるとして、その中に同じアトラクションが複数回含まれると、満足度が低下します。一般に、同じ人に複数回体験させることなく運用するためには、各アトラクションの1日あたりのキャパシティは、パークキャパシティの半分以下に設定すべきです。したがって、以下の条件が必要になります。
8ax2 < 1/2 * ab(x2+xy+y2) ……(4)
少し整理して、
(16-b) x2 – bxy – by2 < 0 ……(5)
です。
また、あまりにも体験可能人数が少なすぎるのも問題です。体験可能人数がパークキャパシティの10%を切って、なおかつ人気アトラクションであれば、整理券を配布しないと混乱が発生するレベルになります。人気アトラクションになるのは、キャパシティが多い側のアトラクションだと考えられます。そこで、体験者数の多いアトラクション体験人数がパークキャパシティの10%以上になるとすると、
8ax2 > 0.1 * ab(x2+xy+y2) ……(6)
少し整理して、
(b-80)x2 + bxy + by2 < 0 ……(7)
となります。
これらの条件をもとに、アトラクションのキャパシティ設計を考えてみることにしましょう。
アトラクションキャパシティの上下限
まず、式(5)の条件を考えます。bは最大キャパシティのアトラクションの数ですから、日本国内の遊園地で15を超えることは無いと考えられます(米国だとあり得ますが、そうしたパークは営業時間も長いので、結果的にこの項は負になりません)。ここでは、1~5の整数として考えましょう。式(5)をグラフに表示すると、図1のようになります。
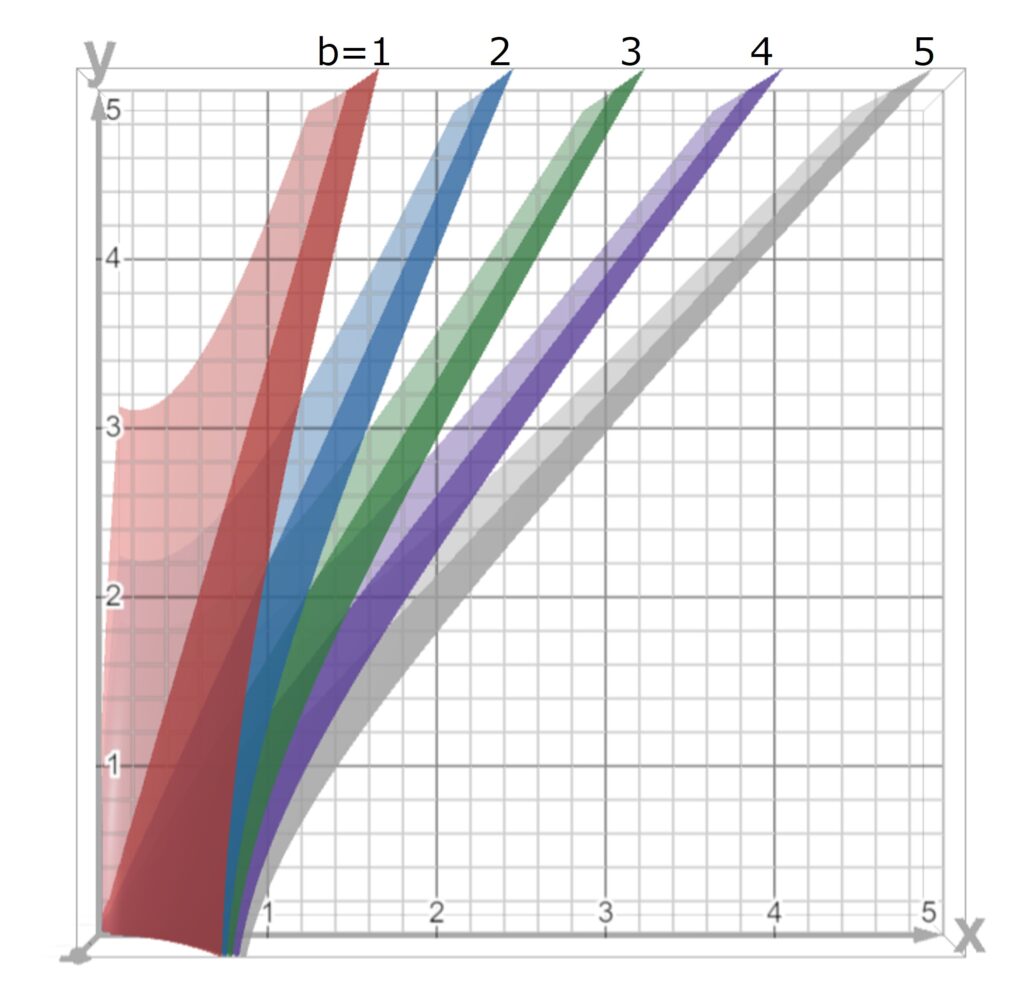
xとbの値を決めた時の、最小のyの値を求めておきましょう。
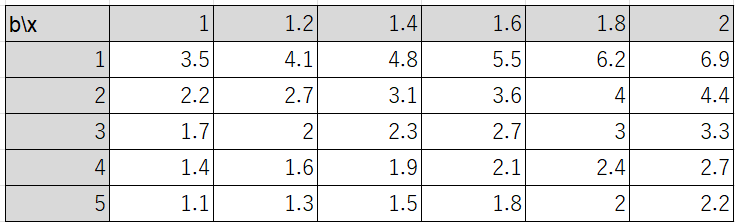
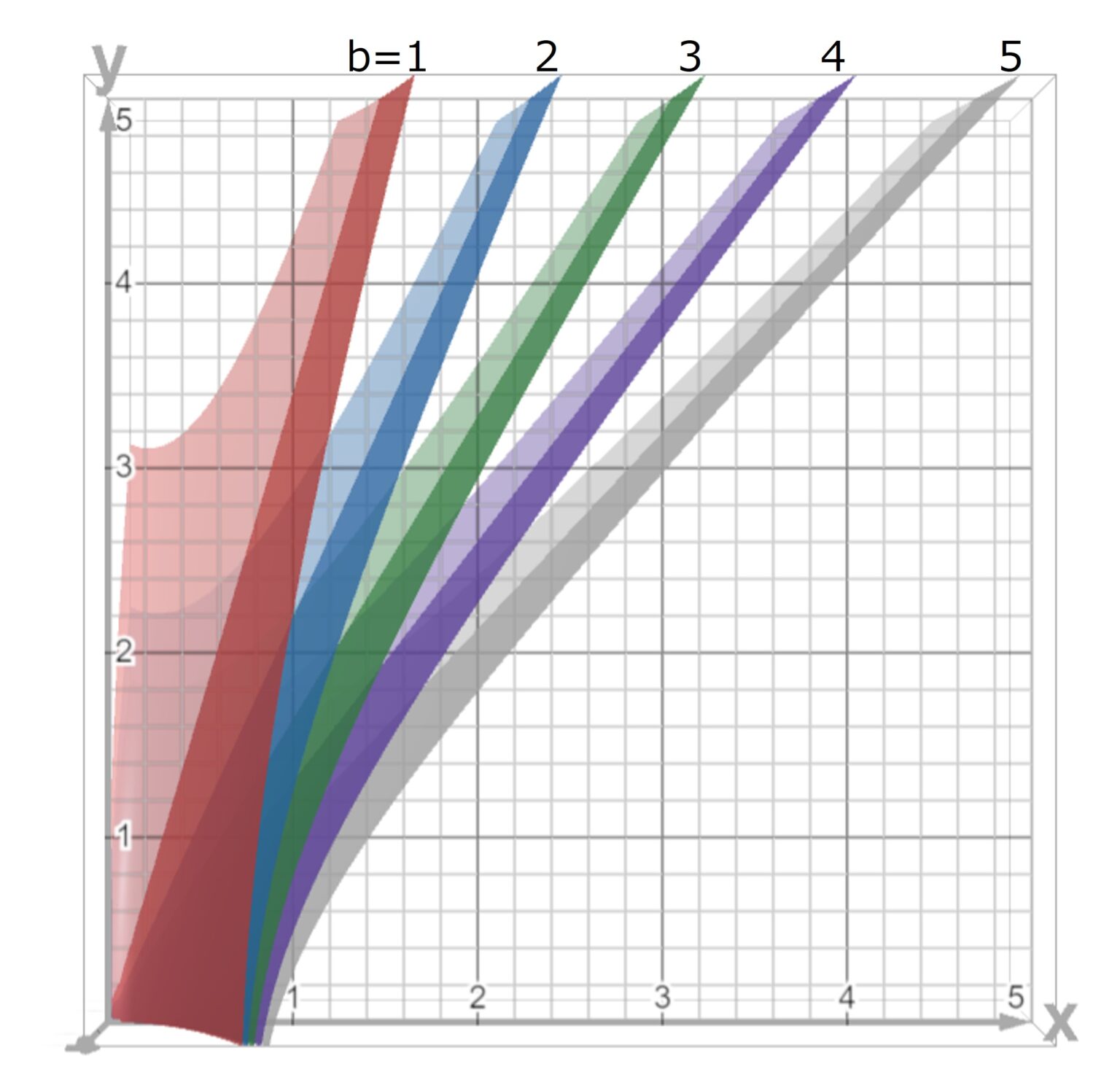
続いて、式(7)の方の条件を確認しておきます。やはり、bが1~5の時のグラフを見てみましょう。図2に示します。
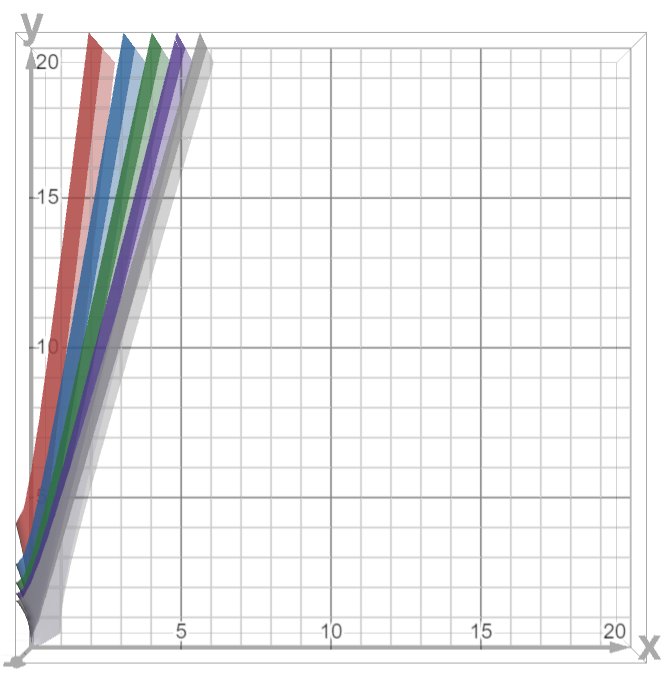
ここから、xとbを決めた時の、yの上限値をいくつか求めておきましょう。
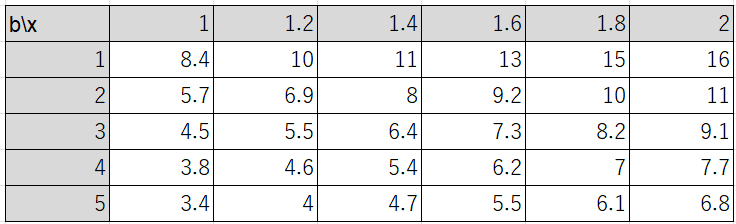
これら2つの条件を満たすx, y の領域は、例えばb=1の場合、以下の図3のようになります。
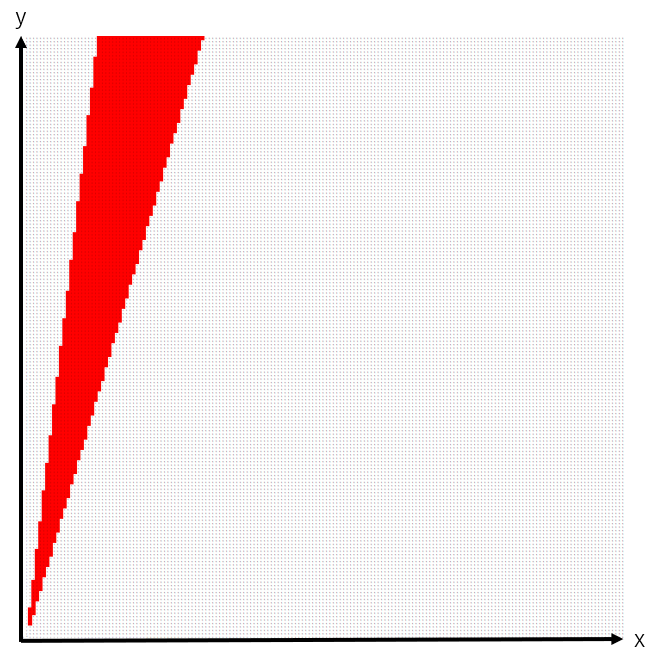
これが、アトラクションのキャパシティに課される制約です。パークのキャパシティをアトラクションのキャパシティによって規制する場合、アトラクションのキャパシティの絶対値に意味は無くて、その相対値のみが制約を受けます。aの項がすべての条件から消えているためです。ただし、アトラクションの数には影響を受けます。
いくつか、架空の例をあげて制約を考えてみましょう。敷地の制約から、設置できるアトラクションは15個以内にしなければいけないとします。b(y2+y+1)≦15です。また、コストの都合で、大きなアトラクションは最大2つしか作れないとします。b≦2です。魅力度の観点から、bはできるだけ大きく取りたいので、b=2としましょう。このとき、y≦2.1となります。by2, by, bのすべてが整数である必要がありますので、ここではy=2とします。アトラクション数は、小さいアトラクションが8個、中規模が4個、大型が2個と決まりました。この時、式(5)と式(7)を満たすx(x>1)の値がありませんので、このようなパークは成立しないことになります。x>1とすると、大型アトラクションのキャパシティが過剰になってしまいます。なお、b=1でも成立しません。解決策は、小型アトラクションを増やす、乗車回数の期待値を下げる、あるいは営業時間を延ばすことです。
同じような比率ですが、全アトラクション数が70の場合を考えてみましょう。かなり極端な例です。b=10として、小型40個、中型20個、大型10個を設置します。すると、1<x<5の範囲で成立するようになります。大型アトラクションが増えれば、パークキャパシティに占める、1つの大型アトラクションの割合が低下しますので、成立しやすくなります。
キャパシティ設計の考え方
以上から得られた知見をまとめておきましょう。
- 大型アトラクションが少ないと、キャパシティが歪になる
- 大型アトラクションが少ないパークは、営業時間を長く取り、その中で2回転以上させることを目指すべき
- アトラクションごとのキャパシティの比率が大きいと、成立しにくくなる
- 特定のアトラクションを複数回体験する人を減らすため、アトラクションごとのキャパシティの比率は小さい方が良い
- キャパシティ比率が大きい場合は、大型アトラクションを多数導入する必要がある
- 小型アトラクションが少ないと、成立しにくくなる
- パークのキャパシティを増やすために、小型アトラクションはできるだけ多く導入した方が良い
これらの知見は、付加した制約条件から単純に導かれることですが、ある程度定式化・視覚化できることがわかりました。こうした強い制約を念頭に置くことで、アトラクションの導入戦略やパーク設計が考えやすくなると思われます。
引用方法
引用時は、下記を明記してください。
Yu Shioji, J. Amusement Park (2025) 250014.
利益相反
本稿に関わる利益相反はありません。


コメント